Conduction in metals

Charge distribution with in a metal:

To understand the concept of charge distribution with in a metal,let us consider the charge distribution with in sodium as shown in fig.1.,

The plus sign represents the heavy positive sodium nuclei of individual atoms.The heavily shaded regions represent the electrons in sodium atom that are tightly bounded to the nucleus.These are inappreciably distributed as the atoms come together to form a metal.The shaded portion outside the circles contains the valence electrons of an atom in metal.

Thus a metal can be visualized as a region containing a periodic three dimension array of heavy,tightly bound ions permeated with a warm of electrons that may move about quiet freely.This picture is known as the electron-gas description of a metal.

Mean free path:

According to electron-gas theory of a metal,the electrons are in continuous motion.The direction of flight being changed at each collision with heavy(almost stationary) ions.The average distance between collisions is called mean free path.Since the motion is random,then,on an average,there will be as many number of electrons passing through unit area in the metal in any direction as in opposite direction in a given time.Hence,the average current is zero.

Drift speed and mobility: 

Let us consider a steady state electric field "" in volt per meter is applied to the metal.The electrons which are moving continuously with in the metal collide with the atoms and rebound in random fashion.Each collision being inelastic i.e., the electron loses some kinetic energy.After the collision,the electron is accelerated and gains certain component f velocity in the direction of  negative electric field and loses its energy at the next collisions.
Thus the applied electric field does not stop collision and random motion but causes the electrons to drift towards the positive terminal.Consequently,the electron gains an average drift velocity  is proportional to the electric field  i.e.,
  where 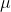 is called electron mobility and it is expressed in square meter/volt-second.
The steady state drift velocity is super imposed on the random motion of electron caused by thermal agitation. This steady flow of electrons in one direction caused by the applied electric field constitutes an electric current.This current is called drift current.

Electric Current and Current density:
Consider a current carrying conductor as shown in below fig., and let us assume that the length of conductor be L , uniform cross section be A,n be the number of electrons passing through the conductor per unit volume i.e., current density and let E be the applied electric field.

Due to this applied,let  be the average or drift velocity of the electrons.The number of free electrons crossing any plane P of cross sectional area in one second is equal to  .

Let q be the charge on each electron,then the charge carried by the electron in one second is .

The electric current (I):

The electric current is defined as the current flowing per second across any national plane of conductor.

Hence , I= 

Conductivity:

                 On combining,

                                        and         J=I/A= qnv

                 we get,

                               

here  represents conductivity of a conductor in (ohm-m)^-1

This is well know Ohm's law.This states that the conduction current is proportional to the applied electric field or the applied electric field or the applied voltage.

Energy distribution of electrons:

If an electron lying inside the metal wanted to escape from the metal,then it must posses an amount of energy at least as great as that  represented by the surface barrier. It is therefore important to know what type of energies are possessed by the electrons in a metal.This relationship is called the energy distribution function or fermi dirac energy distribution.

The fermi dirac statistics enables us to find the no. of free electrons" dn" per unit volume within the energy range E to E+dE at temperature T.

Energy distribution:

The number of free electrons per cubic meter of a metal whose energies lie in the interval E to E+dE is given by,

                              -----------> Eqn 1

where  represents density of electrons in the interval.

In case of free electrons,we can safely assume that there is no potential variation within the metal.Accordingly,each cubic meter of a metal must contain the same no of electrons.Although the electron density in space remain constant within the metal,yet the electrons in each unit volume have all possible energies.The function   represents this distribution in energy.This represents the number of electron volts per cubic meter of the metal.

This function  may be expressed as

                           -----------> Eqn 2

and N(E) is the density of states in conduction band and f(E) is the probability that a quantum state with energy E is occupied by an electron.This function is called as fermi dirac probability function.

The density of states N(E) is bound to be proportional to half power of energy E i.e.,

    or      -------------> Eqn 3

where  is a probability constant.

  "" is defined as

  , -------------> Eqn 4

where m is the mass of the electron in kg and h is planck's constant in Joule-sec.

  Js

According to the principle of quantum mechnics, the fermi dirac probability function is given by,  -----------------> Eqn 5

where    is the energy of electrons, 

            is the fermi level or characteristic energy 

              k  is the Boltzmann's constant 

              T is the temperature

Now  becomes------------> Eqn 6

------------> Eqn 7                   

Fermi -Dirac Function:

Let  us examine the fermi  dirac probability function at T= K we consider the following two possibilities:

i)  :

In this case the exponential term in Eqn 5 becomes zero and hence .

So we have to conclude that all quantum levels with energy less than fermi energy will be occupied at absolute zero.

ii)   :

In this case the exponential term of Eqn 5 becomes infinite and hence .

So there is no probability of finding an occupied quantum state levels of energy greater than fermi energy at absolute zero.

Therefore it may be noted that fermi energy may be defined as the maximum energy that any electron may posses at absolute zero.

Electron emission from a metal:

Emission of electrons is a process in which the free electrons escape from the surface from the surface of a substance.In general metals are used for electron emission because a metal is made up of atoms bound in crystal lattices,of electrons bound to the atoms and of many free electrons which are bounded to any particular location in the metal.The free electrons are always in motion and travel more or less freely throughout the body of the metal.However,these electrons are free only to the extent that they may transfer from one atom to another with in the metal but cannot leave the metal surface

If certain amount of external energy is given to free electron ,its kinetic energy is increased and thus the electron will cross over the surface barrier to escape from the metal.This amount of kinetic energy required at absolute zero temperature is know as work function the metal.It is denoted by  and is expressed in electron-volt(eV).One eV is equal to 1.60*10^-19 Joule,it is the amount of energy required by the electron when it is accelerated through a potential difference of one volt.

The work function of pure metals varies approximately from 2 to 6 eV. The metal used for electron emission should have low work function so that a small amount of external energy is required to cause emission of electrons.Work function of a metal is principally determined by the spacing between its atoms.Wider spacing is generally gives lower values of work function.

Types of electron emission:

The four basic methods of obtaining electron emission from the surface of the metal are classified according to the type of additional energy(equal to the work function of the metal) supplied from the sources such as heat energy,energy stored in electric field,light energy and kinetic energy of the electric charges bombarding the metal surface:

1.Thermionic Emission

2.Field emission

3.Photo-electric emission

4.Secondary emission

1.Thermionic Emission:

When a metal is heated to sufficient temperature,enough thermal energy is imparted to the electrons to enable them to escape from metal surface.The higher the temperature,the greater is the emission of electrons.This method is known as thermionic emission and is employed in vaccum tubes.Richardson and later on,Dush man,on thermodynamic basis derived the equation for thermionic emission at a certain temperature T.

This equation is given by,

                                        

where ,

 is the thermionic emission current in amperes

S is the area of the filament in square meters

 is constant

T is absolute temperature,

k is Boltzmann constant

 is work function,eV

At high temperatures,the electrons are literally being 'boiled' from the metal surface.This is analogous to the boiling of water.

2.Field emission:

When the potential difference between the two electrodes is extremely high,electrons are emitted from the negative electrode,even at ordinary temperatures. If the electric field at the metallic surface of the negative electrodes is of the order of 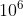 volts per meter,electrons are quiet easily pulled out from the surface.This process of electron emission is employed in cold cathod devices and rectifier tube.

3.Photo-electric emission:

When the surface of certain metals are illuminated by beam of light,electrons are ejected out of certain metals are illuminated by a beam of light,electrons are ejected out of metal by the light photons incident on the metal surface.Such as electron  emission  is known as photo-electric emission and is used in photo-electric cell.The greater the intensity of light beam falling on the metal surface,the greater is the photo-electric emission.

4.Secondary emission:

When a beam of high velocity electrons strike a metal surface,the free electrons are ejected out of the metal.This process is known as secondary emission.

Energies of emitted electrons:

Consider the case of photo emitter and a plane parallel collector.Let a retarding potential be established between them.If all energies electrons leave the cathode with same energy ,the current would remain constant until a definite voltage was reached and then it would fall abruptly to zero.Exponentially no sudden fall is found but the thermionic current for zero retarding voltage is found.

When the barrier height is increased by  ,then the work function becomes  in place of  and we have,

we know that

 

Therefore,

 --------------------------> Eqn 2

Let us assume that this increase in barrier height is caused by application of retarding voltage .

Then

 

This can be written as 

where  can be written as the volt equivalent of temperature and is defined by, ---------------> Eqn 3
here   represents Boltzmann constant in Joule per degree kelvin=1.60*10^-19 k =1.381*10^-5
         k = 8.62*10^-5 eV/k
From equations 2 and 3, we get

So the emitted electrons from the metal also have an energy distribution like the electrons inside the metal.

Disclaimer:
I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.