P-N Junction diode:
P-N junction diode is a two terminal device.It consists of two materials,they are P-type material and N-type material.When a P-type material is intimately joined to N-type material,a P-N junction is formed.In fact merely joining the two materials,a P-N junction cannot be formed because the surface films and other irregularities produce major discontinuities in the crystal structure.
Therefore a P-N junction is formed from a piece of semiconductor by diffusing a P-type material to one half side and N-type material to other half side.The plane dividing the two zones is known as a junction.This P-N junction is formed either in Si or Ge.P-type semi conductors has negative ions and positively charged free holes which move about on P- type semi conductor.Similarly N-type semi conductors has positive donor ions and negatively charged free electrons which move about on N-type.
As the N-type material has high concentration of free electrons and the P-type material has high concentration of holes,therefore,at the junction there is a tendency for the free electrons to diffuse over to the P-side and the holes to diffuse over to the N-side.This process is called diffusion.As the free electrons move across the junction from N-type to P-type,the donor ions becomes positively charged.Hence the positive charge is built on the N-side of the junction.The free electrons that cross the junction,uncover the negative acceptor ions by filling in the holes.Therefore, a net negative charge is established on the P-side of the junction.This negative charge on P-side prevents further diffusion of electrons into the P-side.
Similarly,the net positive charge on the N-side repels the hole crossing from P-side to N-side.Thus,a barrier is set up near the junction which prevents the further movements of charge carriers i.e., electrons and holes.As a consequence of induced electric field across the depletion layer,an electrostatic potential is established between P-region and N-regions,which is called the potential barrier,diffusion potential,junction barrier or contact potential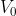 
.The magnitude of this contact potential varies with doping levels and temperature. 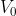is 0.3V for germanium and 0.72V for silicon.
PN junction under zero applied bias:
Here,we will examine the properties of the step junction in thermal equilibrium,where no current exist and no external excitation is applied.We shall also determine the space charge region width,electric field and potential through the depletion region.
a) Built-in potential barrier:
If we assume that ,if no voltage is applied across the p-n junction,then the junction is in thermal equilibrium the Fermi energy level is constant throughout the entire system. the energy band diagram for the p-n junction are in thermal equilibrium. the conduction and valance band energies must bend as we go through the space charge region ,since the relative positions of the conduction and valance bands withe respect to the Fermi energy changes between p and n regions.
Elections in the conduction band of the n region see a potenital barrier in the trying to move into the
conduction band of the p region. this the potential barrier is referred to as the built-in potential barrier and is denoted by
.the build-in potential barrier is referred to as the built-in potential barrier and is denoted by minority carriers electrons in p region, and also between the majority carriers holes in the n-region.this the potential barrier will be formed between the probes and the semi conductor will be cancelled the potential maintains equilibrium, so on current is produced is produced by the volatage.
the intrinsic Fermi level is equidistant from the conduction band edge through the junction, thus the built-in potential barrier can be determined as the difference between the intrinsic Fermi level in p and n region, we can define the potential
and
as shown in fig., so we have
=
----------> eqn (1)
in negative region, the electron concentration inn the conduction band is give by
/KT&space;\right&space;] "n_{o}=n_{c}exp\left [ -(E_{c}-E_{F})/KT \right ]")
-----------> eqn (2)
which can also be written in the form,
/KT&space;\right&space;] "n_{o}=n_{i}exp\left [ (E_{F}-E_{Fi})/KT \right ]")
-----------> eqn (3)
where
and
are the intrinsic carrier concentration and the intrinsic Fermi energy,respectively. we may define the potential 
in the n region as
-------------> eqn (4)
The equation (3) is written as
/KT&space;\right&space;] "n_{o}=n_{i}exp\left [-(ev_{n})/KT \right ]")
-------------> eqn (5)
Taking the natural log both sides of Eq (5),setting the solution
, and solving for the potential,
we obtain
)
---------------> eqn (6)
similarly, in the p region, the holes concentration is given by
-------------------> eqn (7)
where
is the acceptor concentration. we can define the potential 
in the p region as
-----------------> eqn (8)
by combining equation, we find that
 "v_{p}=kT/e ln(N_{a}/n_{i})")
------------------> eqn (9)
Finally, the built-in potential barrier for the step junction is found by substitution Eqs and into Eq which yields
=V_{t}&space;ln(N_{a}N_{d}/n_{i}^{2}) "V_{bi}=kT/e ln(N_{a}N_{d}/n_{i}^{2})=V_{t} ln(N_{a}N_{d}/n_{i}^{2})")
--------> eqn (10)
where
and is defined as the thermal voltage.
b)Calculation of depletion width:
Let us now consider the width of depletion region in the junction as shown in fig., below
The region contains space charge due to the fact that,donors on the N-side and acceptors on P-side have lost their accompanying electrons and holes.Hence an electric field is established, which will inturn would cause a difference in potential energy,
,between the two parts of specimen.Thus,a potential is built up across the junction.
In this analysis,we can observe that there is an abrupt change from acceptor ions on P-side to donor ions on N-side.Assume that the concentration of electrons and holes in depletion region is negligable and that all of the donors and acceptors are ionised.Hence the region of space charge may be described as,
(in this below derivation we consider
)
for P-side
for N-side
,elsewhere
where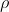
is space charge density.
The potential variation in the space charge region can be calculated in poission's equation,given by,
/\epsilon&space;_{0}\epsilon&space;_{r} "\bigtriangledown ^{2}V= -\rho (x,y,z)/\epsilon _{0}\epsilon _{r}")
The relevant equation for the required one-dimensional problem is
Applying the above equation to the P-side of the junction,we get
On integrating twice,we get,
/2\epsilon&space;_{0}\epsilon&space;_{r})+Cx+D "V=((qN_{A}x^{2})/2\epsilon _{0}\epsilon _{r})+Cx+D")
where C and D are the constants of integration.
If we have V=0 at x=0,and hence D becomes 0.When
on the P-side,the potential is constant,so that 
at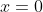 
.
Hence,X_{1} "C=-(qN_{A}/\epsilon _{0}\epsilon _{r})X_{1}")
Therefore,-(qN_{A}/\epsilon&space;_{0}\epsilon&space;_{r}).X_{1}.x "V=(qN_{A}x^{2}/2\epsilon _{0}\epsilon _{r})-(qN_{A}/\epsilon _{0}\epsilon _{r}).X_{1}.x")
i.e.,-(x^{2}/2-X_{1}.x) "V=(qN_{A}/\epsilon _{0}\epsilon _{r})-(x^{2}/2-X_{1}.x)")
As
at 
, we have,
.X_{1}^{2} "V_{1}=-(qN_{A}/2\epsilon _{0}\epsilon _{r}).X_{1}^{2}")
If we apply the same procedure to the N-side,we get,
.X_{2}^{2} "V_{2}=(qN_{D}/2\epsilon _{0}\epsilon _{r}).X_{2}^{2}")
Therefore,the total built-in-potential or contact potential is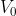 ,where,
(N_{A}X_{1}^{2}+N_{D}X_{2}^{2}) "V_{0}=V_{2}-V_{1}= (q/2\epsilon _{0}\epsilon _{r})(N_{A}X_{1}^{2}+N_{D}X_{2}^{2})")
We know the fact that the positive charge on the N-side must be equal in magnitude to the negative charge on P-side for the neutral specimen.Hence,
PN junction under zero applied bias:
Here,we will examine the properties of the step junction in thermal equilibrium,where no current exist and no external excitation is applied.We shall also determine the space charge region width,electric field and potential through the depletion region.
a) Built-in potential barrier:
If we assume that ,if no voltage is applied across the p-n junction,then the junction is in thermal equilibrium the Fermi energy level is constant throughout the entire system. the energy band diagram for the p-n junction are in thermal equilibrium. the conduction and valance band energies must bend as we go through the space charge region ,since the relative positions of the conduction and valance bands withe respect to the Fermi energy changes between p and n regions.
Elections in the conduction band of the n region see a potenital barrier in the trying to move into the
conduction band of the p region. this the potential barrier is referred to as the built-in potential barrier and is denoted by
 |
| energy band diagram of the p-n junction in therma equilibium |
in negative region, the electron concentration inn the conduction band is give by
which can also be written in the form,
where
The equation (3) is written as
Taking the natural log both sides of Eq (5),setting the solution
we obtain
similarly, in the p region, the holes concentration is given by
where
by combining equation, we find that
Finally, the built-in potential barrier for the step junction is found by substitution Eqs and into Eq which yields
where
b)Calculation of depletion width:
Let us now consider the width of depletion region in the junction as shown in fig., below
 |
| fig., depletion width |
In this analysis,we can observe that there is an abrupt change from acceptor ions on P-side to donor ions on N-side.Assume that the concentration of electrons and holes in depletion region is negligable and that all of the donors and acceptors are ionised.Hence the region of space charge may be described as,
(in this below derivation we consider
where
The potential variation in the space charge region can be calculated in poission's equation,given by,
The relevant equation for the required one-dimensional problem is
Applying the above equation to the P-side of the junction,we get
On integrating twice,we get,
where C and D are the constants of integration.
If we have V=0 at x=0,and hence D becomes 0.When
Hence,
Therefore,
i.e.,
As
If we apply the same procedure to the N-side,we get,
Therefore,the total built-in-potential or contact potential is
We know the fact that the positive charge on the N-side must be equal in magnitude to the negative charge on P-side for the neutral specimen.Hence,
and substituting this relationship in the above equation and using the fact that
Similarly,
The total depletion width,
Junction Voltage:
When the depletion layer is formed,there are negative immobile ions in P-side semiconductor and positive immobile ions in N-type semiconductor as shown in below fig.,
As the negative ions are created on P-side of the junction,so the P-side acquires a negative potential.Similarly,the positive ions on N-side , so on N-side acquires a positive potential.Thus,the initial diffusion of charge carriers creates a potential barrier at the junction.Therefore due to the charge seperation, a voltage V is developed across the junction under equilibrium condition. This voltage is known as junction voltage or internal voltage. This potential voltage is set up in such a manner that results in production of electric field.This electric field prevents the respective minority carriers from crossing the barrier region. The potential barrier is about 0.3V for Ge and 0.7V for Si at room temperature(300K).
Disclaimer:
I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.
Disclaimer:
I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.
No comments:
Post a Comment