Prasanna's blog for electronics: The semiconductors in equilibrium

Equilibrium distribution of electrons and holes:
The distribution of electrons in the conduction band (with respect to energy) is given by the product of density of allowed quantum states and the probability that a state is occupied by the electron.This statement in mathematical form is expressed as,

$n(E)=g_{c}(E)f_{F}(E)$ ----------> eqn.1

Where $f_{F}(E)$ is the fermi dirac probability function and
$g_{C}(E)$ is the density of quantum states in the conduction band

The total electron concentration per unit volume in the conduction band is found by integrating equation 1 over the entire conduction band.

Similarly,the distribution of holes in valence band (with respect to energy) is the density of quantum states in the valence band multiplied by the probability that a state is not occupied by an electron.This is mathematically expressed as,

$p(E)=g_{v}(E)[1-f_{F}(E)]$ -----------> eqn.2
Where $f_{F}(E)$ is the fermi dirac probability function and
$g_{v}(E)$ is the density of quantum states in the valence band
The total hole concentration per unit volume is found by integrating this function over the entire band energy.

To find thermal-equilibrium electron-hole concentrations:

we the we need to determine the position of fermi energy $E_{F}$ with respect to the bottom of conduction band $E_{c}$ and the top of valence band energy $E_{v}$ .In order to address this question,we will initially consider an intrinsic semi conductor.An ideal intrinsic semi conductor is a pure semi conductor with no impurity atoms and no lattice defects in the crystal(e.g., pure silicon). Since for an intrinsic semi conductor at T=0K,all energy states in the valence band are filled with electrons and all energy states in the conduction band are empty electrons.Therefore the fermi energy lies in between Ec and Ev.

As the temperature begins to increase above above 0K,the valence electrons will gain thermal energy.A few electrons in the valence band may gain sufficient energy to jump to the conduction band.As the electron jump from the valence band to conduction band,an empty state,or hole is created in the valence band.In the intrinsic semi conductor,then,electrons and holes are created in pairs by the thermal energy so that the number of electrons in the conduction band is equal to the number of holes in valence band.

fig a.,density of state functions,fermi dirac probability function and areas representing electron and hole concentration near the mid gap energy

In the above fig shows a plot of the density states function in the conduction band $g_{c}$ (E) the density of states function in the valence band $g_{v}(E)$ and the Fermi - Dirac probability function function for T>0 K when $E_{F}$ is approximately halfway between $E_{c}$ and $E_{v}$ .if we assume for the moment that the electron and hole effective masses are equal then $g_{c}E$ and $g_{v}(E)$ are symmetrical functions about the midgap energy (the energy midway between $E_{c}$ and $E_{v}$ .we noted previously that the function $f_{F}$ (E) for $E>E_{F}$ is symmetrical to the function $1-f_{F}(E)$ for $E<E_{F}$ about the energy $E=E_{F}$ . this is also means the function $f_{F}(E)$ for $E=E_{F}+dE$ is equal to the function $1-f_{F}(E)$ for $E=E_{F}-dE$ .

The equilibrium distribution of electrons and holes in intrinsic semiconductors( $n_{0}$ and $p_{0}$ equations for intrinsic semi conductors) :
The fermi energy for an intrinsic semiconductor will be near the midgap. In deriving the equations for thermal-equilibrium concentration of electrons $n_{0}$ and the thermal equilibrium concentration of holes $p_{0}$ , we cannot take this value for granted, because for some particular situations the fermi energy can deviate from this midgap energy.Initially, however, let us assume that the fermi level remains within the bandgap energy.
The equation for the thermal-equilibrium concentration of electrons over the conduction band energy is given by

$n_{0}=\int g_{c}(E)f_{F}(E)dE$ ------------> eqn (3)

The lower limit of integration for above expression should be $E_{c}$ and the upper limit of integration should be the top of the allowed conduction band energy.However,the fermi probability function rapidly approaches zero with the increasing energy.In general,we can take the upper limit as infinity.

Let us assume that the fermi energy is within the forbidden energy band gap. For electrons in the conduction band,
we have $E>E_{c}$

if $E_{c}-E_{f}>>kT$ , then $E-E_{f}>>kT$

so that the fermi probability function reduces to the Boltzmann approximation,which is,

$f_{F}(E)=1/\left ( 1+(exp(E-E_{F})/kT ))\approx exp([-(E-E_{F})]/kT)$ -------------> eqn (4)

Applying the Boltzmann approximation to equation(3) , which is,the thermal - equilibrium density of electrons in the conduction band is found from,

$n_{0}=\int_{E_{c}}^{\propto }( (4\prod (2m_{n}^{*})^{3/2})/h^{3})\sqrt{(E-E_{c})}exp[-(E-E_{c})/kT]dE$ ------------->eqn (5)

The integral of equation (5) may be solved more easily by making a change of variable.If we let,

$\eta =(E-E_{F})/kT$ ------------------> eqn (6)
Then eqn (6) becomes

$n_{0}=4\prod [(2m_{n}^{*}kT )^{3/2})/h^{3}] exp[-(E_{c}-E_{F})/kT]\int_{0}^{\propto }\eta ^{1/2} exp(-\eta )d\eta$ ------------> eqn (7)
we may define a parameter $N_{c}$ as,

$N_{c}= 2(2\prod m_{n}^{*}kT/h^{2})^{3/2}$

So that the thermal-equilibrium electron concentration in the conduction band can be written as

$n_{0}=N_{c}exp[(E_{c}-E_{F})/kT]$ -----------------> eqn (8)

The parameter $N_{c}$ is called the effective density of states function in the conduction band. If we were to assume that $m_{n}^{*}=m_{0}$ ,then the value of the effective density of states function T=300K is $N_{c}=2.5\times 10^{19}cm^{-3}$ , which is of the magnitude of $N_{c}$ for the most semiconductors. If the effective mass of the electron is larger or smaller than $m_{0}$ ,then the value of the effective density of the states function changes accordingly,but is still of the same order of magnitude.

The thermal equilibrium concentration of holes in the valence band in the valence band is given by,

$p_{0}=\int g_{v}(E)[1-f_{F}(E)]dE$ --------------------------> eqn (9)

we may note that,

$[1-f_{F}(E)]dE = 1/(1+exp(E_{F}-E)/kT)$ ----------------> eqn (10.a)

For energy states in the valence band , $E<E_{v}$ . If $(E_{F}-E)>> kT$ ( the fermi is still assumed to be within the band gap),then we have a slightly different form of the Boltzmann approximation. Eqn (10.a) may also be written as,

$1-f_{F}(E)=1/(1+(exp(E_{F}-E)/kT))\approx exp[-(E_{F}-E)/kT]$ ...................> eqn (10.b)

Applying the Boltzmann approximation of eqn(9) to eqn (10.b),we find the thermal-equilibrium concentration of holes in the valence band
$p_{0}=\int_{-\propto }^{E_{v}}(4\prod (2m_{p}^{*})^{3/2} /h^{3})(\sqrt{E_{v}-E})(exp[-(E_{F}-E)/kT])dE$ -------------> eqn(11)
where the lower limit of integration is taken as minus infinity instead of the bottom of the valence band.The exponential term decays fast enough so that this approximation is valid. Eqn (12) may be solved more easily by again making a change of variable.If we let,

$\eta ^{'}=(E_{v}-E)/kT$ ---------------------> eqn (12)
Eqn (11) becomes

$p_{0}=(-4\prod (2m_{p}^{*}kT)^{3/2}/h^{3} )exp[-(E_{F}-E_{v})/kT]\int_{\propto }^{0}(\eta^{'} )^{1/2}exp(-\eta ^{'})d\eta ^{'}$ -----> eqn(12)

where the negative sign comes from the differential $dE=-kTd\eta ^{'}$

Note that the lower the lower limit of $\eta ^{'}$ becomes $+\propto; when E=-\propto$

If we change the order of integration,we introduce another minus sign. Therefore eqn (12) becomes,

$p_{0}=(2\prod m_{p}^{*}kT/h^{2})^{3/2}exp[-(E_{c}-E_{v})/kT]$ ------------> eqn (13)

we may define a parameter $N_{v}$

$N_{v}=2(2\prod m_{p}^{*} kT/h^{3})^{3/2}$ -----------------------> eqn (14)
which is called the effective density of states in the valence band.The thermal-equilibrium concentration of holes in the valence band may now be written as

$p_{0}=N_{v}exp[-(E_{F}-E_{v})/kT]$ ---------------> eqn (15)

Intrinsic carrier concentration:

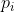For an intrinsic semi conductor,the concentration of electrons in the conduction band is equal to the concentration of holes in the valence band. We may denote $n_{i}$ and $p_{i}$ as the electron and hole concentration ,respectively,in the intrinsic semiconductor.These parameters are usually referred to as the intrinsic electron concentration and intrinsic hole concentration.However,as $n_{i}=p_{i}$ ,so normally $n_{i}$ as the intrinsic carrier concentration,which refers to either intrinsic electron or hole concentration.

The fermi energy level for the intrinsic semi conductor is called the intrinsic fermi energy, or
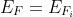
$E_{F}=E_{F_{i}}$

If we apply this value for eqn (8) and (15) to the intrinsic semiconductors,then we can write

$n_{0}=n_{i}=N_{c}exp[-(E_{c}-E_{F_{i}})/kT]$ ------------------> eqn (16)

and

$p_{0}=p_{i}=n_{i}=N_{v}exp[-(E_{F_{i}}-E_{v})/kT]$ ----------------> eqn(17)

If we take the product of eqns (16) and (17),we obtain,

$n_{i}^{2}=N_{c}N_{v}exp[-(E_{c}-E_{F_{i}})/kT]exp[-(E_{F_{i}}-E_{v})/kT]$ ------------> eqn (18)

or

$n_{i}^{2}=N_{c}N_{v}exp[-(E_{c}-E_{v})/kT]=N_{c}N_{v}exp[-(E_{g})/kT]$ -------------> eqn (19)

where $E_{g}$ is the band gap energy. For a given semi conductor material at a constant temperature,the value of $n_{i}$ is constant and independent of the fermi level.

The intrinsic carrier concentration for Silicon at T=300 K may be calculate by using effective density of states function values of $N_{c},N_{v}, m_{n}^{*}/m_{0},m_{p}^{*}/m_{0}$ .

The commonly accepted value of $n_{i}$ for silicon at T=300K is approximately 1.5*10^-3. This discrepancy may arise from several sources.First, the values of the efffective masses are determined at low temperature where the cyclotron resonance experiments are performed.Since the effective mass is an experimentally determined parameter and also a measure of how well the particle moves in the crystal,,therefore,this parameter can be considered as a function of time. Next,the state functions for a semi conductor was obtained by generalizing the model of an electron in a three-dimensional infinite potential well.But this theoretical function is not exactly agreed with the experiment.

However,the difference between the theoretical value and the experimental values of $n_{i}$ is approximately a factor of 2,which ,in many cases is not significant.

The intrinsic fermi-level position:
As we have studied that the fermi energy level is located near the center of the forbidden band gap for intrinsic semi conductor,now,we can specifically calculate the intrinsic fermi-level position.Since the electron and hole concentration are equal, let us set eqn(16) and (17) equal to each other.
Therefore,we have,

$N_{c}exp[-(E_{c}-E_{F_{i}})/kT]= N_{v}exp[-(E_{F_{i}}-E_{v})/kT]$ -------------------> (20)

If we take the natural log of both sides of this equation and solve for $E_{F_{i}}$ ,we obtain,

$E_{F_{i}}=(1/2)(E_{c}+E_{v})+(1/2)(kT)ln(N_{v}/N_{c})$ -----------------------> (21)

From the definitions of $N_{c}$ and $N_{v}$ the equation (21) is written as,

$E_{F_{i}}=[(1/2)(E_{c}+E_{v})]+[(3/4)(kT)(m_{p}^{*}/m_{n}^{*})]$ --------------------> (22.a)

The first term, $[(1/2)(E_{c}+E_{v})]$ , is the energy exactly midway between $E_{c},E_{v}$ , or the mid gap energy.

Therefor we can define $(1/2)(E_{c}+E_{v})=E_{midgap}$

so that, $(E_{F_{i}}-E_{midgap})=(3/4)kTln(m_{p}^{*}/m_{n}^{*})$ -------------> (22.b)

If the electron and hole effective masses are equal so that $m_{p}^{*}=m_{n}^{*}$ ,then the intrinsic fermi level is exactly in the center of the band gap.

If $m_{p}^{*}>m_{n}^{*}$ ,the intrinsic fermi level is slightly above the center .

If $m_{p}^{*}<m_{n}^{*}$ ,the intrinsic Fermi level is slightly below the center of the band gap.

The density of state function is directly related to the carrier effective mass.Thus a larger effective mass means a larger density of state functions.The intrinsic fermi level must shift away from the band with larger density of states in order to maintain equal number of electrons and holes.

The equilibrium distribution of electrons and holes in extrinsic semi conductor(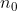 $n_{0}$ and $p_{0}$ equations for extrinsic semiconductors ):

On adding donor or acceptor impurity atoms to a semi conductor,these impurity atoms will change the distribution of electrons and holes in the material.Since,the fermi energy is related to the distribution he function,the fermi energy will change as per the dopant atoms added. If the fermi level changes from near the mid gap value,the density of holes in the valence band will change.These effects are shown in below figures.


fig.1 and fig.2

Fig 1., shows the case for $E_{F}>E_{F_{i}}$ ,the electron concentration is larger than the hole concentration. and fig 2., shows the case for $E_{F}< E_{F_{i}}$ ,the hole concentration is larger than the electron concentration.When the density of electron is greater than the density of holes, the semiconductor is n-type; donor impurity atoms have been added and when the density of holes are greater than the density of electrons, the semiconductor is p-type; acceptor impurity atoms have been added.

The Fermi energy level in a semi conductor changes as the electron and hole concentration change,and again,the Fermi energy changes as donor or acceptor impurities are added. The change in the Fermi level as a function of impurity concentrations will be considered for charge neutrality.

The expressions previously derived for the thermal-equilibrium concentration of electrons and holes given by

$n_{0}=N_{c}exp[-(E_{c}-E_{F})/kT]$

and

$p_{0}=N_{v}exp[-(E_{F}-E_{v})/kT]$

Now,we shall derive another form of equations for the thermal-equilibrium concentrations of electrons and holes.If we add and subtract an intrinsic Fermi energy in the exponent of above equation for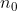 $n_{0}$ ,we can write

$n_{0}=N_{c}exp[(-(E_{c}-E_{F_{i}})+(E_{F}-E_{F_{i}}))/kT]$ -------------> (23.a)

or

$n_{0}=N_{c}exp[-(E_{c}-E_{F_{i}})/kT]exp[(E_{F}-E_{F_{i}})/kT]$ --------------> (23.b)

The intrinsic carrier concentration is given by

$n_{i}=N_{c}exp[-(E_{c}-E_{F_{i}})/kT]$

so that the thermal-equilibrium electron concentration can be written as
$n_{0}=n_{i} [exp[-(E_{c}-E_{F_{i}})/kT]]$

Similarly,if we add and subtract an intrinsic Fermi energy in the exponent of above $p_{0}$ , we will obtain
$p_{0}=n_{i}exp[-(E_{F}-E_{F_{_{i}}}/kT )]$

The $n_{0}p_{0}$ Product:
The product of the general expressions for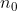 $n_{0}$ and $p_{0}$ is expressed as,

$n_{0}p_{0}=N_{c}N_{v}exp[-(E_{c}-E_{F})/kT]exp[-(E_{F}-E_{v})/kT]$ ------------------> (24)

which may be written as,
$n_{0}p_{0}=N_{c}N_{v}exp[-E_{g}/kT]$

Disclaimer:

I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.

2 comments:

Sam Smith20 May 2019 at 15:20
Chem Academy offers IIT JAM Coaching Classroom courses now in Jaipur. According to student review and our results Chem Academy is known as Best IIT Jam Coaching In India and Best CSIR Net Coaching In India. PHYSICS and Chemistry New Batches Starting from April. IIT JAM Coaching Classroom courses Share extraordinary data about your blog , Blog truly accommodating for us . We read your blog , share most helpful data in blog . A debt of gratitude is in order for offer your blog here .

Prasanna's blog for electronics

Monday, 14 August 2017

The semiconductors in equilibrium

2 comments:

pn junction diode part- 1