Introduction:
 ,then the drift current density is given by
,then the drift current density is given by
 --------------> eqn (1)
--------------> eqn (1)
where J is in units of or
or 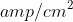
If the volume charge density is due to positively charged holes then
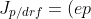v_{dp}) ---------------> eqn(2)
---------------> eqn(2)
where is the drift current density due to holes and
is the drift current density due to holes and  is the average drift velocity of the holes.
is the average drift velocity of the holes.
The equation of motion of a positively charged hole in the presence of an electric field is
 ------------------> eqn(3)
------------------> eqn(3)
where e is the magnitude of the electronic charge, a is the acceleration, E is the electric field and is the effective mass of the hole.
is the effective mass of the hole.
 ------------------> eqn(4)
------------------> eqn(4)
By combining eqns (2)and (4) we may write the drift current density due to holes as
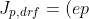v_{dp}=e\mu&space;_{p}pE) --------------->eqn(5)
--------------->eqn(5)
The drift current due to holes is in the same direction as the applied electric field.
The same discussion of drift applies to electrons. We may write
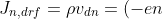v_{dn}) ------------------->eqn(6)
------------------->eqn(6)
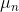 is the electron mobility and is a positive quantity. now the above but one equation (6) can written as
is the electron mobility and is a positive quantity. now the above but one equation (6) can written as
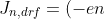(-\mu&space;_{n}E)=e\mu&space;_{n}nE) -------------->eqn(8)
-------------->eqn(8)
Mobility Effects:
Hole mobility is given as
The net flow of electrons and holes in a semi conductor will generate current.The process by which these charged particles move is called transport. In this post we shall consider the two basic transport mechanisms in a semi conductor crystal; drift-the movement of charge due to the electric fields and diffusion. In addition to these basic phenomena, the temperature gradients in a semi conductor can also lead to carrier movement .However, as the semiconductor devices size becomes smaller, this effect can usually be ignored. The carrier transport phenomena are the foundation for finally determining the current-voltage characteristics of semiconductor.
Carrier Drift:
When an electric field is applied to a semiconductor ,then it will produce a force on electrons and holes so that they experience a net acceleration and net movement ,provided ,there should be available energy states in the conduction and in the valance bands. This net movement of charge due to an electric field is called drift. The net drift of charge gives rise to the concept of drift current.
Drift current density:
If we have a positive volume charge density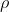 moving at an average drift velocity
moving at an average drift velocity
When an electric field is applied to a semiconductor ,then it will produce a force on electrons and holes so that they experience a net acceleration and net movement ,provided ,there should be available energy states in the conduction and in the valance bands. This net movement of charge due to an electric field is called drift. The net drift of charge gives rise to the concept of drift current.
Drift current density:
If we have a positive volume charge density
where J is in units of
If the volume charge density is due to positively charged holes then
where
The equation of motion of a positively charged hole in the presence of an electric field is
where e is the magnitude of the electronic charge, a is the acceleration, E is the electric field and
If the electric field is constant then we except the velocity to increase linearly with time. However, when the charged particles in the semiconductor are involved in collisions or scattering events, then the velocity characteristics of the particles are altered.
As the hole accelerates in a crystal due to the electric field, the velocity increases. When the charged particle collides with an atom in the crystal ,for example,if the particle loses most or all of its energy.,then the particle will again begin to accelerate and gain energy until it is gets involved in the scattering process. This continues over and over again. Throughout this process the particle will again an average drift velocity which for low electric fields is directly proportional to the electric field. we may therefore write as,
where 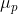 is the proportionality factor and is called the hole mobility.The mobility is an important parameter of the semiconductor since it describes how well a particle will move due to an electric field. The unit of mobility is usually expressed in terms of
is the proportionality factor and is called the hole mobility.The mobility is an important parameter of the semiconductor since it describes how well a particle will move due to an electric field. The unit of mobility is usually expressed in terms of  .
.
By combining eqns (2)and (4) we may write the drift current density due to holes as
The drift current due to holes is in the same direction as the applied electric field.
The same discussion of drift applies to electrons. We may write
where  is the drift current density due to electrons and
is the drift current density due to electrons and  is the average drift velocity of electrons . The net charge density of electrons is negative.
is the average drift velocity of electrons . The net charge density of electrons is negative.
The average drift velocity of an electron is also proportional to the electric field for small fields. However, since the electron is negatively charged the net motion of the electron is opposite to the electric field direction.We can then write
where
The conventional drift current due to electrons is also in the same direction as the applied electric field even through the electron movement is in the opposite direction.
Electron and hole mobilities are functions of temperature and doping concentrations.Since both electrons and holes contribute to the drift current, the total drift current density is the sum of the individual electron and hole drift current densities, so we may write
Mobility Effects:
In the last section, we defined mobility which relates the average drift velocity of a carrier to the electric field.Electron and hole mobilities are important semiconductor parameters in the characterization of carrier drift,as seen in eq(9).
Figure shows a schematic model of the random thermal velocity and motion of a hole in a semiconductor with zero electric field.There is a mean time between collisions which may be donated by 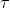 . If small electric field (E-field) is applied as indicated in fig 4.1(b), there will be a net drift of the holes in the direction of the E-field, and the net drift velocity will be a small perturbation on the random thermal velocity, so the time between collisions will not be altered appreciably.
. If small electric field (E-field) is applied as indicated in fig 4.1(b), there will be a net drift of the holes in the direction of the E-field, and the net drift velocity will be a small perturbation on the random thermal velocity, so the time between collisions will not be altered appreciably.
Hole mobility is given as
where
Similarly, electron mobility is given by
where
There are two types of collision or scattering mechanisms that dominate in a semiconductor and affect the carrier mobility: phonon or lattice scattering , and ionized impurity scattering.
Phonon Scattering:
The atom in a semiconductor crystal have certain amount of thermal energy at temperatures above absolute zero that causes the atoms to randomly vibrate about their lattice equation within the crystal. The lattice vibrations cause a disruption in the perfect periodic potential function.A perfect periodic potential in a solid allows electrons to move unimpeded, or with no scattering, through the crystal. But the thermal vibrations cause a disruption of the potential function, resulting in an interaction between the electrons or holes and the vibrating lattice atoms. This lattice scattering is also referred to as photon scattering.
Since lattice scattering is related to the thermal motion of atoms, the rate at which the scattering occurs is a function of temperature. If we denotes  as the mobility that would be observed if only lattice scattering existed, then the scattering theory states that to first order
as the mobility that would be observed if only lattice scattering existed, then the scattering theory states that to first order
Mobility that is due to lattice scattering increase as the temperature decrease. Intuitively, we expect the lattice vibrations to decrease as the temperature decreases, which implies that the probability
of a scattering event also decrease, thus increasing mobility.
Impurity Scattering:
The second interaction mechanism affecting carrier mobility is called ionized impurity scattering.We have seen that impurity atoms are added to the semiconductor to control or alter its characteristics. These impurities are ionized at room temperature so that a coulomb interaction exists between the electrons or holes and the ionized impurities.This coulomb interaction produces scattering or collisions and also alters the velocity characteristics of the charge carrier. If we denote  as the mobility that would be observed if only ionized impurity scattering existed then to first order we have
as the mobility that would be observed if only ionized impurity scattering existed then to first order we have
If temperature increases, the random thermal velocity of a carrier increases, reducing the time the carrier spends in the vicinity of the ionized impurity center. The less time spent in the vicinity of a coulomb force, the smaller the scattering effect and the larger the expected value of  . If the number of ionized impurity centers increases, then the probability of a carrier encountering an ionized impurity center increases, implying a smaller value of
. If the number of ionized impurity centers increases, then the probability of a carrier encountering an ionized impurity center increases, implying a smaller value of  .
.
If  is the mean time between collisions due to lattice scattering, then
is the mean time between collisions due to lattice scattering, then  is the probability of a lattice scattering event occurring in a differential time dt. Like wise , if
is the probability of a lattice scattering event occurring in a differential time dt. Like wise , if  is the mean time between collisions due to ionized impurity scattering, then
is the mean time between collisions due to ionized impurity scattering, then  is the probability of an ionized impurity scattering event occurring in the differential time dt. If these two scattering processes are independent, then the total proability of a scattering event occurring in the differential time dt is the sum of the individual events, or
is the probability of an ionized impurity scattering event occurring in the differential time dt. If these two scattering processes are independent, then the total proability of a scattering event occurring in the differential time dt is the sum of the individual events, or
where Comparing eqn (14) with the definitions of mobility given by eqn (10) or eqn(11),we can write
where  is the mobility due to the ionized impurity scattering process and
is the mobility due to the ionized impurity scattering process and  is the mobility due to the lattice scattering process.
is the mobility due to the lattice scattering process.
The parameter 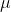 is the net mobility. With two or more independent scattering mechanisms, the inverse mobilities add, which means that the net mobility decreases.
is the net mobility. With two or more independent scattering mechanisms, the inverse mobilities add, which means that the net mobility decreases.
Conductivity:
The drift current density,given by eqn (9) may be written as
where
We have just seen that the motilities are function of impurity concentrations;conductivity, then is a somewhat complicated function of impurity concentration. Resistivity(ohm-cm) is given as
If we have a bar of semiconductor material as shown Fig 4.3 with a voltage applied that produces a current I, then we can write
J=I/A ----------------> eqn(17a)
and E=V/L ---------------> eqn(17b)
We can now rewrite eqn(16) as
Equation(4.18b) is ohm's law for a semiconductor. The resistance is a function of resistivity, or conductivity, as well as the geometry of the semiconductor.
If we consider for example, a p-type semiconductor with an acceptor doping
Similarly for n-type semiconductor current density is given by
So, for same amount of doping, same electric field and at same temperature
V-I Characteristics:
Consider an intrinsic semiconductor bar. If an electric field is applied then with the increase of electric field drift velocity of carrier increases which increases the current. But after a certain limit, with increase of electric field is increased to a very high value then electrons gain a very large energy. When they collide with semiconductor atoms they remove more electrons i.e., excess carriers are generated. At this point, the current increases very rapidly. This process is known as impact ionization.
[ As in intrinsic semiconductor, both carriers are of the same concentration]
Then drift current will be much more as compared to the intrinsic one.
For an n-type semiconductor with  ,the current will be more than the p-type one for the some condition as
,the current will be more than the p-type one for the some condition as  .
.
Carrier Diffusion:
There is a second mechanism, in addition to drift, that can induce a current in a semiconductor. We may consider a classic physics example in which a container, as shown in Fig 4.11, is divided into two parts by a membrane.The left side contains gas molecules at a particular temperature and the right side is initially empty. The gas molecules are in continual random thermal motion so that, when the membrane is broken, the gas molecules flow into the right side of the container. Diffusion is the process whereby particles flow from a region of high concentration toward a region of low concentration. If the gas molecules were electrically charged, the net flow of charge would result in a diffusion current.
Diffusion Current Density:
Fig 4.13(a) shows the variation of electron concentration with distance. Due to this concentration gradient diffusion current flows.
Electron diffusion current density proportional to charge gradient,
where
The diffusion of holes, f
rom a negative x direction. Since holes are positively charged particles, the conventional diffusion current density is also in the negative x direction. The holes diffusion current density is proportional to the hole density gradient and to the electronic charge, so we may write
for the one-dimensional case. The parameter
Total Current Density:
We now have four possible independent current mechanisms in a semiconductor. These components are electron drift and diffusion currents and hole drift and diffusion currents.
The total current density is the sum of these four components, or, for the one-dimensional case:
Total current density = Electron drift current + hole drift current + electron diffusion current + hole diffusion current.
This equation may be generalized to three dimensions as
The expression for the total current in a semiconductor contains four terms. Fortunately in most situations, we will only need to consider one term at any one time at a particular point in a semi conductor.
Graded Impurity Distribution:
In most cases so far, we have assumed that the semiconductor is uniformly doped. In many semiconductor devices, however, there may be regions that are non uniformly doped. We will investigate how a non uniformly doped semiconductor reaches thermal equilibrium and from this analysis we will derive the Einstein relation which relates mobility and the diffusion coefficient.
Induced Electric Field:
Consider a semiconductor that is non uniformly doped with donor impurity atoms. If the semiconductors is in thermal equilibrium the Fermi energy level is constant through the crystal.The doping concentration decreases as x increases in this case. There will be a diffusion of majority carrier electrons from the region of high concentration to the region of low concentration, which is in the +x direction.
The flow of negative electrons leaves behind positively charged donor ions. The separation of positive and negative charge induces an electric field that is in a direction to oppose the diffusion process. When equilibrium is reached, the mobile carrier concentration is not exactly equal to the fixed impurity concentration and the induced electric field prevents any further separation of charge. In most cases of interest, the space charge induced by this diffusion process is a small fraction of the impurity concentration, thus the mobile carrier concentration is not too different from the impurity dopant density.
The electric field for the one-dimensional situation is defined as
If the intrinsic Fermi level changes as function of distance through a semiconductor in thermal equilibrium an electric field exists in the semiconductor.
If we assume a quasi-neutrality condition in which the electron concentration is almost equal to the donor impurity concentration then we can still write
solving for
The Fermi level is constant for thermal equilibrium so when we take the derivative with respect to x we obtain
The electric field can then be written combing eqs (29) and (26) as
Since we have an electric field, there will be a potential differences through the semiconductor due to the non uniform doping.
The Einstein Relation:
If we consider the non uniformly doped semiconductor represented by the energy-band diagram shown in fig 4.14 and assume there are no electrical connections so that the semiconductor is in thermal equilibrium, then the individual electron and hole currents must be zero. we can write
If we assume quasi-neutrality so that
Substituting the expression for the electric field from eq(4.30) into eq(4.32), we obtain
Equation (4.33) is valid for the condition
The hole current must also be zero in the semiconductor. From this condition, we can show that
Combining eqs (4.34a) and (4.34b) gives
The diffusion coefficient and mobility are not independent parameters. This relation between the mobility and diffusion coefficient, given by eq(4.35), is known as the
Einstein relation. The diffusion coefficient is approximately 40 times smaller than the mobility at room temperature.
As
The Hall Effect:
The Hall effect is a consequence of the forces that are exerted on moving charges by electric and magnetic fields. The Hall effect is used to distinguish whether a semiconductor is n type or p type and to measure the majority carrier concentration and majority carrier mobility. The Hall effect device, as discussed in this section is used to experimentally measure semiconductor parameters. However, it is also used extensively in engineering applications as a magnetic probe and in other circuit applications.
The force on a particle having a charge q and moving in a magnetic field is given by
F=qv*B------------->eqn(36)
Where the cross product is taken between velocity and magnetic field so that the force vector is perpendicular to both the velocity and magnetic field.
A semiconductor with a current  is placed in a magnetic field perpendicular to the current. In this case, the magnetic field is in the z direction. Electrons and holes flowing in the semiconductor will experience a force as indicated in the figure. The force on both electrons and holes is in the (-y) direction. In a p-type semiconductor
is placed in a magnetic field perpendicular to the current. In this case, the magnetic field is in the z direction. Electrons and holes flowing in the semiconductor will experience a force as indicated in the figure. The force on both electrons and holes is in the (-y) direction. In a p-type semiconductor ) there will be a build up of positive charge on the y=0 surface of the semiconductor and in an n-type semiconductor
there will be a build up of positive charge on the y=0 surface of the semiconductor and in an n-type semiconductor
F=q[E+ v*B]=0 ---------------->eqn(37a)
which becomes
The induced electric field in the y-direction is called the Hall field.The Hall field produces a Voltage across the semiconductor which is called the Hall voltage. We can write
In a p-type semiconductor in which holes are the majority carrier the Hall voltage will be positive . In an n-type semiconductor in which electrons are the majority carrier the Hall voltage will have the opposite polarity. The polarity of the Hall voltage is used to determine whether an extrinsic semiconductor is n-type or p-type.
Substituting eq (38) into eq (37) gives
For a p-type semiconductor the drift velocity of holes can be written as
Or solving for the hole concentration we obtain
The majority carrier hole concentration is determined from the current magnetic field and Hall voltage. For p-type semiconductor Hall coefficient is given by
For an n-type semiconductor the Hall voltage is given by
so that the electron concentration is
Note that the Hall voltage is negative for the n-type semiconductor,therefore,the electron concentration can be determined from eq (44) is actually a positive quantity.For n-type semiconductor Hall coefficient is given as
Once the majority carrier concentration has been determined,immediately we can calculate the low field majority carrier mobility. For a p-type semiconductor , we can write
The current density and electric field can be converted to current and voltage, so that the above eqn becomes
The hole mobility is the given by
Similarly for an n-type semiconductor the low-field electron mobility is determined from
Disclaimer:
I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.




No comments:
Post a Comment