Charge carriers in semi conductors:
![p= \gamma [e^{(E_{v}-E_{F})/kT}]\int_{-\propto }^{0}(kT)^{1/2}x^{1/2}e^{-x(-kT)}dx](https://latex.codecogs.com/gif.latex?p=&space;\gamma&space;[e^{(E_{v}-E_{F})/kT}]\int_{-\propto&space;}^{0}(kT)^{1/2}x^{1/2}e^{-x}(-kT)dx)
^{3/2}\int_{0}^{\propto }x^{1/2}e^{-x}dx](https://latex.codecogs.com/gif.latex?p=&space;\gamma&space;[e^{(E_{v}-E_{F})/kT}](kT)^{3/2}\int_{0}^{\propto&space;}x^{1/2}e^{-x}dx)
Current is defined as the rate at which the charge flows.In a semi conductor,both the electrons and holes can contribute current.As the current represents represents the density of charge carriers,let us now study about an important characteristic of semi conductor which is called the density of charge carriers.the density of electrons and holes is related to the density of states function and the fermi distribution function both of which we have considered.The fermi dirac statistics enables us to find the no of free electron  per unit volume within the energy range E to E+dE at temperature T.
per unit volume within the energy range E to E+dE at temperature T.
Energy distribution;
The no of free electrons per cubic meter of a metal whose energies lie in the interval E to E+dE is given by
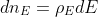
where represents the density of electrons in this interval.
represents the density of electrons in this interval.
In case of free electrons we can safely assume that there is no potential variation within the metal.Accordingly each cubic meter of a metal must contain the same no of electron . although the electron density in space remains constant within the metal yet the electrons in each unit volume have all possible energies.
The function represents this distribution in energy. This represents the no of electrons volt per cubic metric of the metal.
represents this distribution in energy. This represents the no of electrons volt per cubic metric of the metal.
The function may be expressed as
may be expressed as
 = N(E)f(E)
= N(E)f(E)
where N(E) is the density of states in conduction band and
f(E) is the probability that a quantum state with energy E is occupied by an electron.
This function is called as fermi dirac probability function.
The density of states N(E) is bound to be proportional to half power of energy E i.e
\alpha&space;E\tfrac{1}{2})
=\gamma&space;E^{1/2})
where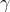 is proportionality constant and is defined as
is proportionality constant and is defined as
^{3/2}/h^{3}) = 6.82*10^27
= 6.82*10^27
According to the principle of quantum mechanics,the fermi dirac probability function is given by,
=1/\left&space;(&space;1+exp\left&space;\{&space;(E-E_{F})&space;/kT\right&space;\}&space;\right&space;))
where ,
E is the energy of electrons in eV
 is the fermi level or characteristic energy in eV
is the fermi level or characteristic energy in eV
k is the Boltzmann's constant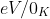
T is the temperature in degree k
Now,
&space;/kT\right&space;\})
&space;/kT\right&space;\})
Fermi level for an intrinsic semi conductors:
In an intrinsic semi conductors,the number of electrons is equal to the number of holes.Therefore the concentration of electrons decreases above the bottom of conduction band and similarly the concentration of holes decreases below the top of valence band
The examination of above fig., shows that the centre of gravity of electrons and holes lies exactly at the middle of forbidden gap.The central level is known as fermilevel. Thus fermi level is the energy level that corresponds to the centre of gravity of the conduction electrons and holes weighted according to their energies.
******Carrier concentration in Intrinsic semi conductors:******
To calculate the conductivity of a semi conductor,it is necessary to know the concentration of free electrons "n" in conduction band and conduction of holes in valence band.
The aim of this article is to calculate the following:
a) number of electrons in conduction band
b) number of holes in valence band
c) fermi level in intrinsic semi conductors
d) intrinsic concentration of charge carriers
e) carrier concentration in terms of band energy
a) Number of electrons in conduction band:
Inorder to calculate the number of electrons in conduction band of an intrinsic semi conductors,the following points should be kept in mind:
i)The number of conduction electrons, dn per cubic meter whose energies lies between E to E+dE is given by,
dn= N(E)f(E) dE ----------> eqn (1)
where N(E) is the density of states
f(E) is the fermi function
ii)The density of states of states N(E) is given by the expression
=\gamma&space;E^{1/2})
Here we have assumed that the bottom of conduction band is at zero potential.In a semi conductor the lowest energy in conduction band is Ec and hence the above equation can be modified as,
=\gamma&space;(E-E_{c})^{1/2}&space;for&space;E>E_{c}) ---------------> eqn (2)
---------------> eqn (2)
iii)The fermi function f(E) is given by,
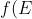=1/(1+exp\left&space;\{&space;(E-E_{F}/kT&space;\right&space;\}))
where is the energy of fermi level.
is the energy of fermi level.
For in conduction band and
in conduction band and  in valence band ,we have
in valence band ,we have
fig., 1(c) shows the variation of fermi function f(E) versus E,both for 0k and at room temperature are as shown in fig c., It is obvious that the probability of finding an electron in conduction band is zero i.e., f(E) = 0 while the probability of finding a hole in valence band is zero i.e., 1-f(E)=0.
fig., 1(d) represents the concentration of electrons in conduction band which is the area under the curve and is given by,
f(E)dE) ----------> eqn( 4)
----------> eqn( 4)
Substituting the values of N(E) and f(E) in above equation,we get,
^{1/2}e^{-(E-E_{F})/kT}) ---------------> eqn (5)
---------------> eqn (5)
where
^{3/2}/h^3)
^{3/2}(1.602\times&space;10^{-19})/h^3)
Equation 5 can now be written as,
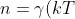^{1/2}\int_{-\propto&space;}^{\propto&space;}((E-E_{c})/kT)^{1/2}e^{-(E-E_{c}+E_{c}-E_{F})/kT}dE)
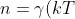^{1/2}\int_{-\propto&space;}^{\propto&space;}((E-E_{c})/kT)^{1/2}e^{-(E-E_{c})/kT}e^{-(E_{c}-E_{F})/kT}dE)
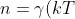^{1/2}e^{-\left&space;(&space;E_{c}&space;-E_{F}/kT\right&space;)}\int_{+E_{c}&space;}^{\propto&space;}((E-E_{c})/kT)^{1/2}e^{-(E-E{c})/kT}dE)
Now,
put![[(E-E_{c})/kT]=x](https://latex.codecogs.com/gif.latex?[(E-E_{c})/kT]=x) or
or 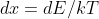
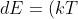dx)


![n= \gamma (kT)^{1/2}[e^{-(E_{c}-E_{F})/kT}]\int_{0}^{\propto }x^{1/2}e^{-x}(kT)dx](https://latex.codecogs.com/gif.latex?n=&space;\gamma&space;(kT)^{1/2}[e^{-(E_{c}-E_{F})/kT}]\int_{0}^{\propto&space;}x^{1/2}e^{-x}(kT)dx)
![n= \gamma (kT)^{3/2}[e^{-(E_{c}-E_{F})/kT}]\int_{0}^{\propto }x^{1/2}e^{-x}dx](https://latex.codecogs.com/gif.latex?n=&space;\gamma&space;(kT)^{3/2}[e^{-(E_{c}-E_{F})/kT}]\int_{0}^{\propto&space;}x^{1/2}e^{-x}dx)
^{1/2}}) /2](https://latex.codecogs.com/gif.latex?n=&space;\gamma&space;(kT)^{3/2}[e^{-(E_{c}-E_{F})/kT}](\sqrt{(3.14)^{1/2}})&space;/2)
Now,
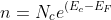/kT}) --------------> eqn (6)
--------------> eqn (6)
where
![N_{c}=\gamma (kT)^{3/2}[\sqrt{\pi }/2]](https://latex.codecogs.com/gif.latex?N_{c}=\gamma&space;(kT)^{3/2}[\sqrt{\pi&space;}/2])
(2m_{e})^{3/2}(1.602\times&space;10^{-19})^{3/2}(kT)^{3/2}(\sqrt{\pi&space;}/2))
(1.602\times&space;10^{-19})^{3/2})
^{3/2}) --------------> eqn( 7)
--------------> eqn( 7)
Here k is given in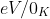
while is expressed in joule per degree kelvin.
is expressed in joule per degree kelvin.
Therefore, the number of electrons in conduction band,is given by,
^{3/2}e^{-(E-E_{F})/kT}) -----------------> eqn (8)
-----------------> eqn (8)
2.Number of holes in valence band:
To derive the expression for the hole concentration in valence band,the following points are to be remembered:
i) The density of states is given by,
=\gamma&space;(E_{v}-E)^{1/2}&space;for&space;E<E_{v}) ---------------> eqn (9)
---------------> eqn (9)
ii) Since a hole is created by removal of an electron i.e., formation of empty level,the fermi function of hole is [1-f(E)].Here f(E) represents the probability that the level is occupied by an electron.Thus the probability function becomes,
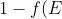=1-1/(1+e^{(E-E_{F})/kT}))
![=1-[(1+e^{(E-E_{F})/kT})]^{-1}](https://latex.codecogs.com/gif.latex?=1-[(1+e^{(E-E_{F})/kT})]^{-1})
![=1-[(1-e^{(E-E_{F})/kT})]](https://latex.codecogs.com/gif.latex?=1-[(1-e^{(E-E_{F})/kT})])
/kT}) ---------------> eqn (10)
---------------> eqn (10)
The number of holes per cubic meter in valence band is given by,
![p=\int_{-\propto }^{E_{v}}N(E)[1-f(E)]dE](https://latex.codecogs.com/gif.latex?p=\int_{-\propto&space;}^{E_{v}}N(E)[1-f(E)]dE) ---------------> eqn (11)
---------------> eqn (11)
Sub the values of N(E) and [1-f(E)] in eqn (11),we get,
^{1/2}e^{(E-E_{F})/kT}dE)
^{1/2}e^{(E_{v}-E_{F}+E-E_{v})/kT}dE)
/kT}\int_{-\propto&space;}^{E_{v}}(E_{v}-E)^{1/2}e^{(E-E_{v})/kT}dE) ----------------> eqn 12
----------------> eqn 12
let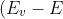/kT=x)
Then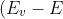=xkT)
Now,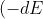=(kT)dx)
Substitute these values in eqn 12,we get,
Energy distribution;
The no of free electrons per cubic meter of a metal whose energies lie in the interval E to E+dE is given by
where
In case of free electrons we can safely assume that there is no potential variation within the metal.Accordingly each cubic meter of a metal must contain the same no of electron . although the electron density in space remains constant within the metal yet the electrons in each unit volume have all possible energies.
The function
The function
where N(E) is the density of states in conduction band and
f(E) is the probability that a quantum state with energy E is occupied by an electron.
This function is called as fermi dirac probability function.
The density of states N(E) is bound to be proportional to half power of energy E i.e
where
According to the principle of quantum mechanics,the fermi dirac probability function is given by,
where ,
E is the energy of electrons in eV
k is the Boltzmann's constant
T is the temperature in degree k
Now,
Fermi level for an intrinsic semi conductors:
In an intrinsic semi conductors,the number of electrons is equal to the number of holes.Therefore the concentration of electrons decreases above the bottom of conduction band and similarly the concentration of holes decreases below the top of valence band
The examination of above fig., shows that the centre of gravity of electrons and holes lies exactly at the middle of forbidden gap.The central level is known as fermilevel. Thus fermi level is the energy level that corresponds to the centre of gravity of the conduction electrons and holes weighted according to their energies.
******Carrier concentration in Intrinsic semi conductors:******
To calculate the conductivity of a semi conductor,it is necessary to know the concentration of free electrons "n" in conduction band and conduction of holes in valence band.
The aim of this article is to calculate the following:
a) number of electrons in conduction band
b) number of holes in valence band
c) fermi level in intrinsic semi conductors
d) intrinsic concentration of charge carriers
e) carrier concentration in terms of band energy
a) Number of electrons in conduction band:
Inorder to calculate the number of electrons in conduction band of an intrinsic semi conductors,the following points should be kept in mind:
i)The number of conduction electrons, dn per cubic meter whose energies lies between E to E+dE is given by,
dn= N(E)f(E) dE ----------> eqn (1)
where N(E) is the density of states
f(E) is the fermi function
ii)The density of states of states N(E) is given by the expression
Here we have assumed that the bottom of conduction band is at zero potential.In a semi conductor the lowest energy in conduction band is Ec and hence the above equation can be modified as,
iii)The fermi function f(E) is given by,
where
For
Here ,
fig., 1(a) shows that the energy band diagram for intrinsic semi conductor.The top of the energy level of valence band and the bottom of energy levels of conduction band are designated as Ev and Ec respectively.
fig., 1(b) shows that ,at room temperature,few electrons get excited to higher energies.At few states near the bottom of conduction band are filled as,in the shown in fig.,b .Further at room temperature, in the upper region of valence band,the upper region of valence band,the probability of occupancy of states get decreased slightly below unity. This is due to the fact that some of the electrons have got shifted to conduction band.fig., 1(c) shows the variation of fermi function f(E) versus E,both for 0k and at room temperature are as shown in fig c., It is obvious that the probability of finding an electron in conduction band is zero i.e., f(E) = 0 while the probability of finding a hole in valence band is zero i.e., 1-f(E)=0.
fig., 1(d) represents the concentration of electrons in conduction band which is the area under the curve and is given by,
Substituting the values of N(E) and f(E) in above equation,we get,
where
Equation 5 can now be written as,
Now,
put
Now,
where
Here k is given in
while
Therefore, the number of electrons in conduction band,is given by,
2.Number of holes in valence band:
To derive the expression for the hole concentration in valence band,the following points are to be remembered:
i) The density of states is given by,
ii) Since a hole is created by removal of an electron i.e., formation of empty level,the fermi function of hole is [1-f(E)].Here f(E) represents the probability that the level is occupied by an electron.Thus the probability function becomes,
The number of holes per cubic meter in valence band is given by,
Sub the values of N(E) and [1-f(E)] in eqn (11),we get,
let
Then
Now,
Substitute these values in eqn 12,we get,
where,
Therefore the number of holes in valence band is given by,
eqn (15) gives the concentration of holes in valence band.
3.Fermi level in intrinsic semi conductors:
Equations (6) and (13) are applicable to both intrinsic as well as intrinsic as well as extrinsic semi conductors.In case of intrinsic semi conductors,the subscript i is added to n and p.Therefore
and
Since the semi conductor crystal is electrically neutral,we have,
substitute these values in (6) and (13),we get,
Taking log on both sides,we have,
If the effective mass of electron is equal to effective mass of hole i.e.,
then Nc is equal to Nv.
eqn 19 shows that fermi level is exactly half way between the top of valence band and bottom of conduction band,i.e., at the center of forbidden energy gap.
*Number of electrons in conduction band in terms of energy gap
The number of electrons in conduction band is given by,
we know that,
Adding these equations,we get,
Sub the values of
*Number of holes in valence band in terms of band gap
The number of holes in valence band is given by,
we know that,
and
On subtracting these equations,we get,
substitute the values of
4.Intrinsic concentration of charge carriers:
On multiplying equation 6 and 14, we get the product of electron-hole concentration i.e.,
This product is independent of the fermi level
Equation (20) is applicable to intrinsic as well as extrinsic semi conductors.For intrinsic semi conductor
and
Thus
This relation is known as mass action law.
Equation (21) states that in any semi conductor regardless the donor or acceptor concentration or the magnitude of n and p,the product np is always constant.
From equation 7,we have,
or
From equation 14,we have,
Substitute these values in equation 20,we get,
The variation of
where,
Therefore substitute the values of k1 and k2 in eqn( 24),we get,
5.Carrier concentration in terms of Band Gap:
i) Fermi level when
For an intrinsic semi conductor,the electrons and holes are always generated in pairs,hence,
or
Taking log on both sides,we have:
ii)Number of electrons in conduction band in terms of band
From equation (A).,
We know that
iii)Number of holes in valence band in terms of energy gap
From equation (A):
We know that,
From equations (B) and (C),we conclude that the density of electrons in conduction band is equal to density of holes in valence band.Further the value of n and p increases exponentially as temperature increases.
Since we have calculated the value of n and p, it is found that
From this value let us calculate electrical conductivity.
Electrical conductivity:
The conductivity of intrinsic semi conductor is given by,
where
Further,
For n=p,
let
Now, substituting the values of n,we get,
Here the values of n,is taken as mass of the electron which is different from mass of the hole.
Fermi level for an extrinsic semi conductor:
The below diagrams indicate the fermi level with donor impurity and acceptor impurity respectively.,
Fermi level with donor impurity:
When a donor impurity is added to an intrinsic semi conductor,it becomes N-type.Now,it has more conduction electrons than holes.This moves the center of gravity up i.e., fermi level shifts towards the conduction band.
Fermi level with acceptor impurity:
When an acceptor impurity is added to an intrinsic semi conductor,it becomes P-type.Now it has more number of holes than electrons.This moves the center of gravity down i.e., fermi level shift towards the valence band.
******Carrier concentration of extrinsic semiconductor:******
1.Fermi level in N-type extrinsic semi conductor:
Consider a donor type impurity and let us add this impurity to a crystal and all donor atoms are ionized at a given temperature.Here the first  states are filled.Due to these filled states,it becomes difficult for the valence band electrons to bridge the energy gap by thermal agitation.We know that fermi level is a measure of probability of occupancy of the allowed energy states.Hence the fermi level must move closer to indicate that many energy states in that band are filled by the donor electrons and fewer holes are filled by the donor electrons and fewer holes exist in valence band.
states are filled.Due to these filled states,it becomes difficult for the valence band electrons to bridge the energy gap by thermal agitation.We know that fermi level is a measure of probability of occupancy of the allowed energy states.Hence the fermi level must move closer to indicate that many energy states in that band are filled by the donor electrons and fewer holes are filled by the donor electrons and fewer holes exist in valence band.
>No of electrons in N-type semi conductors:
The n type semi conductors constitute electrons which are almost entirely filled with extrinsically supplied electrons from the donor and hence  ,where
,where  is the concentration of donor atom.
is the concentration of donor atom.
substitute
On solving we get,
2.Fermi level in P-type extrinsic semi conductor:
Here it is assumed that:
i) The density of acceptor atom far exceeds the density of donor atom.
ii) Every acceptor has accepted one electron from valence band.
iii)The density of electrons in conduction band is much smaller than the density of holes in valence band.This leads to conclusion that fermi level must move from center of forbidden gap closer to valence band for a p-type.
>No of holes in P-type semi conductor:
The p-type semi conductors constitute holes which are almost entirely filled with extrinsically supplied holes from the acceptor ,hence  ,where
,where  is the concentration of acceptor atom.
is the concentration of acceptor atom.
On solving,we get,
Here, it should be remembered that as the temperature of either N-type or P-type material increases,the fermi level moves towards the center of energy gap.
Disclaimer:
I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.





No comments:
Post a Comment