Prasanna's blog for electronics: August 2017

Introduction:

When a voltage is appiled or a current exists in a semi conductor device,the semiconductor is said to be operating under non-equilibrium conditions.Excess electrons in the conduction band and excess holes in valence band may exist in addition to the thermal-equilibrium concentrations if an electric excitation field is applied to the semi conductor.This post introduces the behaviour of non equilibrium electron and hole concentration as functions of time and space coordinates.

Carrier generation and recombination:

Generation is the process whereby electrons and holes are created and recombination is the process where by electrons and holes are eliminated.Any deviation of semi conductor,from thermal equilibrium will tend to change its electron and hole concentrations.

Thermal generation rates and recombination rates of semi conductor in equilibrium:
In thermal- equilibrium,the concentration of electrons in conduction band and the concentration of holes in valence band,respectively are independent of time.However,electrons are continually being thermally excited from the valence band into the conduction band by random nature of the thermal process.At,the same time,electrons moving randomly through the crystal in the conduction band may come in close proximity to holes and fall into the empty states in valence band.This recombination process annihilates both the electrons and holes.Since,the net carrier concentration are independent of time in thermal equilibrium,the rate at which they recombine must be equal.

Let $G_{n_{0}}$ and $G_{p_{0}}$ be the thermal-generation rates of electrons, respectively, given in units of $cm^{-3}s^{-1}$ .For the direct band-to-band generation, the electrons and holes in pairs,so we must have that, $G_{n_{0}}=G_{p_{0}}$ .

Let $R_{n_{0}}$ and $R_{p_{0}}$ be the combination rates of electrons and holes,respectively,for a semi conductor in thermal equilibrium.

In direct band-to-band recombination,electrons and holes recombine in pairs,so that,
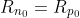
$R_{n_{0}}=R_{p_{0}}$

In thermal equilibrium,the concentrations of electrons and holes are independent of time;therefore,the generation and recombination rates are equal,so we have,
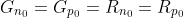
$G_{n_{0}}=G_{p_{0}}=R_{n_{0}}=R_{p_{0}}$

Excess Carrier Generation and Recombination:
Excess carrier generation and recombination take place when the electrons in valence band may be excited into the conduction band,when,for example,higher energy photons are incident on semi conductor.When this happens an electron is created in the conduction band and also a hole is created in the valence band;thus an electron hole pair is generated. These additional electrons and holes which are so created are called excess electrons and excess holes.
When a semi conductor is in nonequilibrium,then excess carriers may be generated in the semi conductor.If in thermal equilibrium,carriers concentration is $n_{i}$ ,then $n_{i}>n$ .Basically,there are three types of generation and they are the following:
(i) Photogeneration:
In photogeneration,light of wavelength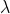 $\lambda$ falls on a semi conductor and if hv i.e., the energy of light is greater than the band gap of the semiconductor then one electron will jump from valence band to conduction band generating an electron-hole pair.

The above figure shows that by absorbing light of energy $hv(>E_{g})$ electrons of the valence band go to the conduction band leaving a hole in the valence band.For different wavelengths of light with different energies $(hv_{2},hv_{3})$ it can take an electron in higher conduction band states.

ii) Phonon Generation:
Photon generation occurs when a semi conductor is under thermal excitation.With increase of temperature of the semi conductor,lattice vibrations increase which gives rise to more photons.Due to more lattice vibrations covalent bonds in semi conductor breaks down and electron-hole pairs are generated.

iii) Impact Ionization:
In this process,one energetic charge carrier will create another charge carrier.When a semi conductor is under the electric field,then the electrons gain sufficient energy from the applied electric field between two successive collisions and hit other Si atoms.In this process,a bond breaks out generating more carriers.For a very high electric field,it results in avalanche breakdown.

In recombination,a pair of electron and hole gets annihiliated. It doesnot mean that they are destroyed,but when a free electron in the conduction band falls into the valence band and recombines with a hole,it becomes bound electron in the whichvalence band.

Characteristics of excess carriers:
The generation and recombination rates of excess carriers are important parameters,but the way the excess carriers behave with time and space in the presence of electric fields and density gradients is of equal important.As the excess electrons and holes donot move independently of each other but they diffuse and drift with the same effective diffusion coefficient and with the same effective mobility.This phenomenon is called ambipolar transport equation.
To understand the concepts of excess carrier diffusion coefficients and effective mobility which characterizes the behavior of these excess carriers,first we have to develop the continuity equations for carriers and then develop ambipolar transport equations.

Continuity Equation:
The continuity equation states a condition for dynamic equilibrium for the density of mobile carriers in any elementary volume of the semi conductor.We know that on disturbing the equilibrium concentrations of carriers in a semi conductor,the concentrations of holes or electrons vary with time approaching the equilibrium value exponentially.
In general,the carrier concentration in the body of semiconductor is a function of both time and distance.The differential equation governing this functional relationship is called continuity equation.This equation is based on the fact that the charge can neither be created or be destroyed.

To find the continuity equations for electrons and holes let us consider a differential volume element in which a one dimensional hole-pair flux entering the differential element at x is leaving the element at x+dx. The parameter $F_{px}^{+}$ is the hole particle flux,or flow,and has units of number of holes/cm^2-s.

For the x component of the particle,the current density is as written as shown below.,

$F_{px}^{+}(x+dx)=F_{px}^{+}(x)+\frac{\partial(F_{px}^{+}) }{\partial x}dx$ -----------------> eqn(1)

This equation corresponds to Taylor's expansion of $F_{px}^{+}(x+dx)$ ,where the differential length dx is small,so that only the first two terms in the expansion are significant.The net increase in the number of holes per unit time without the differential volume element due to the x-component of the hole flux is given by,

$\frac{\partial p }{\partial t}dxdydz=[F_{px}^{+}(x)-F_{px}^{+}(x+dx)]dydz=-\frac{\partial F_{px}^{+} }{\partial x}dxdydz$ -----------> eqn(2)

If $F_{px}^{+}(x)>F_{px}^{+}(x+dx)$ ,then there will be a net increase in the number of holes in the differential volume element with time.

The generation rate and recombination rate of holes will also affect the concentration in the differential volume.The net increase in the number of holes per unit time in the differential volume element is then given by,

$\frac{\partial p}{\partial t}dxdydz=-\frac{\partial F_{px}^{+}}{\partial x}dxdydz+g_{p}dxdydz-(p/\tau _{pt})dxdydz$ ------------------>eqn(3)

where p is the density of holes.The first term on the right side of eqn(3) is the increase in the number of holes per unit time due to the hole flux,the second term is the iny crease in the number of holes per unit time due to the generation of holes,and the last term is the decrease in the number of holes per unit time due to the recombination of holes.The recombination rate for holes is given by $p/\tau _{pt}$ ,where $\tau _{pt}$ includes the thermal equilibrium carrier lifetime and the excess carrier life time.

If we divide both sides of the eqn(3) by the differential volume dxdydz,the net increase in the hole concentration per unit time is

$\frac{\partial p}{\partial t}=-\frac{\partial F_{p}^{+}}{\partial x}+g_{p}-p/\tau _{pt}$ ------------------------> eqn(4)

Equation (4) is known as continuity equation for holes.

Similarly,the one-dimensional continuity equation for electrons is given by,

$\frac{\partial n}{\partial t}=-\frac{\partial F_{n}^{-}}{\partial x}+g_{n}-n/\tau _{nt}$ ---------------------->eqn (5)

Time-Dependent Diffusion Equations:
Let us once again note down the equations for one-dimensional hole and electron current densities,which are as follows :

$J_{p}=e\mu _{p}pE-eD_{p}\frac{\partial p}{\partial x}$ -------------------> eqn(1)

$J_{n}=e\mu _{n}pE+eD_{n}\frac{\partial n}{\partial x}$ --------------------> eqn(2)
If we divide the hole current density by (+e) and the electron current density by (-e),we obtain each particle flux.These equations becomes

$J_{p}/(+e)=F_{p}^{+}=\mu _{p}pE-D_{p}\frac{\partial p}{\partial x}$ -----------------> eqn(3)

and

$J_{n}/(-e)=F_{n}^{+}=-\mu _{n}nE-D_{n}\frac{\partial n}{\partial x}$ --------------------> eqn(4)

Taking the divergence of eqns (3) and (4),and substituting these equations in continuity equations,we get.,

$\frac{\partial p}{\partial t}=-\mu _{p}\frac{\partial (pE)}{\partial x}+D_{p}\frac{\partial^2 p}{\partial x^2}+g_{p}-p/\tau _{pt}$ --------------------> eqn(5)

and

$\frac{\partial n}{\partial t}=\mu _{n}\frac{\partial (nE)}{\partial x}+D_{n}\frac{\partial^2 n}{\partial x^2}+g_{n}-n/\tau _{nt}$ -----------------------> eqn(6)

Since we are limiting ourselves to one-dimensional analysis,we can expand the derivative of the product as,

$\frac{\partial (pE)}{\partial x}=E\frac{\partial p}{\partial x}+p\frac{\partial E}{\partial x}$ ----------------------------> eqn (7)

In a more generalized three dimensional analysis, eqn (7) is replaced by a vector identity and the eqns(5),(6) can be written in the form,
$D_{p}\frac{\partial^2 p}{\partial x^2}-\mu _{p}(E\frac{\partial p}{\partial x}+p\frac{\partial E}{\partial x})+g_{p}-p/\tau _{pt} =\frac{\partial p}{\partial t}$ ------------------> eqn(8)

and

$D_{n}\frac{\partial^2 n}{\partial x^2}+\mu _{n}(E\frac{\partial n}{\partial x}+n\frac{\partial E}{\partial x})+g_{n}-n/\tau _{nt} =\frac{\partial n}{\partial t}$ -------------------> eqn(9)

The hole and electron concentrations are functions of both the thermal equilibrium and the excess values.For the special case of homogeneous semiconductor,the thermal equilibrium concentrations are also independent of eqn(8) and (9).Thus they can be written as,

$D_{p}\frac{\partial^2 (\delta p)}{\partial x^2}-\mu _{p}(E\frac{\partial (\delta p)}{\partial x}+p\frac{\partial E}{\partial x})+g_{p}-(p/\tau _{pt})=\frac{\partial (\delta p)}{\partial t}$ --------------------> eqn(10)

$D_{n}\frac{\partial^2 (\delta n)}{\partial x^2}+\mu _{n}(E\frac{\partial (\delta n)}{\partial x}+n\frac{\partial E}{\partial x})+g_{n}-(n/\tau _{nt})=\frac{\partial (\delta n)}{\partial t}$ ---------------------> eqn(11)

Note:
The equations (10) and (11) contain terms involving the total concentrations,p and n,and terms involving only excess concentrations.

Ambipolar transport:
If a pulse of excess electrons and a pulse of excess holes are created at a particular point in semiconductor within an applied electric field,the excess holes and electrons will tend to drift in opposite directions.However,ass the electrons and holes are charged particles,any separation will induce an internal electric field will create a force attracting the electrons and holes back towards each other.Then the electric field term in above eqns (10) and (11),is then composed of the externally applied field plus the induced internal field.This E- field may be written as,

$E=E_{app}+E_{ext}$ ------------------------>eqn(12)
where Eapp is the applied electric field and Eext is the induced electric field.

Since the internal electric field creates a force attracting the electrons and holes,this electric field will hold the pulses of excess electrons and excess holes together.Then the negatively charged electrons and the positively charged holes will drift together with a single effective mobility or diffusion coefficient.This phenomenon is called ambipolar diffusion or ambipolar transport.

Derivation of ambipolar transport equation:

The time dependent diffusion eqns (10) and (11),describe the behaviour of the excess carriers.However a third equation is required to relate the excess electron and hole concentrations to the internal electric field.This relation is Poisson's equation,which may be written as,

$\triangledown .E=[e(\delta p-\delta n)/\epsilon _{s}]=\frac{\partial E_{int}}{\partial x}$ -----------------------> eqn (13)
where $\epsilon _{s}$ is the permittivity of semiconductor material.

To make the solution of eqns (10),(11),(13) more tractable,we need to make some approximations.We can show that only a relatively small internal electric field is sufficient to keep the excess electrons and holes drifting and diffusing together.Hence,we assume that,

$\left | E_{int} \right |<<\left | E_{app} \right |$ -----------------------> eqn (14)

However,the $\bigtriangledown . E_{int}$ term may not be negligable. Let us impose the condition of charge neutrality and let us assume that the excess electron concentration is just balanced by an equal to excess hole concentration at any point in space and time.If these assumptions were exactly true,there would be no induced internal electric field to keep the two sets of particle together.However,the small difference in the excess electron concentration and the hole concentration will set up an internal E-field sufficient to keep the particle diffusing and drifting together.We can show that one percent difference in $\delta p,\delta n$ .

We can combine Eqns (11) and (12) to eliminate the $\bigtriangledown .E$ term.

We can write thermal generation of electrons and holes as,

$g_{n}=g_{p}=g$ -------------------------> eqn (15)

and also let us also define the recombination rates of electrons and holes as,

$R_{n}=(n/\tau _{nt})=R_{p}=(p/\tau _{pt})=R$ ---------------------> eqn(16)

The lifetimes in eqn(16) induces the thermal-equilibrium carrier lifetimes.If we impose the charge neutrality condition,then $\delta n=\delta p$ .We will denote both the excess electron concentration and excess hole conceantration in eqns (10) and (11) by $\delta n$ .We may then rewrite, eqns (10) and (11) as

$D_{p}\frac{\partial^2 (\delta n)}{\partial x^2}-\mu _{p}(E\frac{\partial(\delta n) }{\partial x}+p\frac{\partial E}{\partial x})+g-R=\frac{\partial(\delta n) }{\partial t}$ ----------------------> eqn (17)

and

$D_{n}\frac{\partial^2 (\delta n)}{\partial x^2}+\mu _{n}(E\frac{\partial(\delta n) }{\partial x}+n\frac{\partial E}{\partial x})+g-R=\frac{\partial(\delta n) }{\partial t}$ ------------------------> eqn(18)

If we mutiply eqn (17) by $n\mu _{n}$ and multiply eqn(18) by $p\mu _{p}$ ,and add the two equations,the

$(\bigtriangledown .E)=\frac{\partial(E) }{\partial x}$ term will be eliminated.The result of this addition gives,

$(n\mu _{n}D_{p}+p\mu _{p}D_{n})\frac{\partial^2 (\delta n)}{\partial x^2}+(\mu _{n}\mu _{p})(p-n)E\frac{\partial (\delta n)}{\partial x}+(n\mu _{n}+p\mu _{p})(g-R)=(n\mu _{n}+p\mu _{p})\frac{\partial (\delta n)}{\partial t}$
------------------------->eqn(19)

If we divide eqn (19) by the term $(n\mu _{n}+p\mu _{p})$ ,this equation becomes,

$D^{'}\frac{\partial^2 (\delta n)}{\partial x^2}+\mu ^{'}E\frac{\partial (\delta n)}{\partial x}+g-R=\frac{\partial (\delta n)}{\partial t}$ ------------------------->eqn(20)

where,

$D^{'}= (n\mu _{n}D_{p}+p\mu _{p}D_{n})/(n\mu _{n}+p\mu _{p})$ ----------------------------> eqn (21)

and

$\mu ^{'}= (\mu _{n}\mu _{p}(p-n))/(n\mu _{n}+p\mu _{p})$ -------------------------> eqn(22)

Eqn (20) is called the ambipolar transport equation and describes the behavior of the excess electrons and holes in time and space.The parameter $D^{'}$ is called the ambipolar diffusion coefficient and $\mu ^{'}$ is called the ambipolar mobility.

The Einstein relation relates the mobility and diffusion coefficient by,

$\mu _{n}/D_{n} =\mu _{p}/D_{p}=e/kT$ --------------------------->eqn(23)

Using these relations,the ambipolar diffusion coefficient may be written in the form,

$D^{'}=D_{n}D_{p}(n+p)/nD_{n}+pD_{p}$ ----------------------------------> eqn(24)

Disclaimer:
I have created this blog for educational purpose,so for that i have written the content by referring many books,web pages.I have also uploaded google images and you tube videos for the better understanding of concept and I would also like to inform you that I am not responsible for the ads which are being posted in my blog.

Prasanna's blog for electronics

Tuesday 29 August 2017

Non equilibrium excess carriers in semi conductors

pn junction diode part- 1